Understanding Spatial Locality of Reference
Spatial Locality of Reference: an Efficient Access Pattern in any Cache System
The sequence in which you access data can have major performance implications. For example, when iterating over a two dimensional array stored in row-major order, looping by x first and then by y can be up to 6.5 times slower than looping by y first and then by x.
Simply changing the order in which you loop while accessing memory can dramatically reduce execution time:
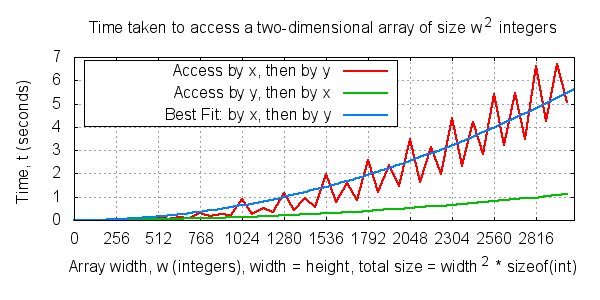
Full benchmark details are given in a following section.
I will later give an example of a real world application that experienced a full 650% speedup due to this approach.
The difference comes from the way you access contiguous memory in the loop. By reading memory in sequential order, memory access is faster. This phenomenon is known as locality of reference.
Locality of Reference
Locality of reference, also known as the principle of locality, is an access pattern that can improve the efficiency of caches in any system.
Most computer systems have several cache systems implemented in hardware alone: the newest consumer-market CPUs have three layers of cache. Therefore, the implications of an efficient access pattern in a cache is important to improving the performance of virtually any computer program.
A cache system in this context uses a dedicated section of memory to source data from a slower medium, so that future requests for that data can be served faster from the cache. For example, an Operating System will transparently use RAM to cache comparatively slow hard disk data to vastly improve access speed under certain use-patterns.
By exploiting spatial locality of reference -- having data that is stored close together -- it is possible to benefit from a cache system's assumption that if data is accessed, there is a high probability that data nearby will be accessed soon.
This behaviour can be an explicit part of a cache system e.g. a pre-fetch system. It can also be a side-effect of the way data is accessed in blocks, e.g. CPU cache lines, RAM page files, or blocks in data storage.
By minimising the distance between related data, more data can be retrieved from the faster cache (a cache hit) and you minimise the data that has to be retrieved from the slower source (a cache miss).
Optimal spatial locality would apply to data access that is entirely sequential. That is, each time you read the data, each successive element you read is only sizeof(element) bytes distance away in memory, and therefore likely to be in the cache.
This has major implications for the order in which you transverse multi-dimensional arrays.
Detailed Example
Feel free to skip this section and head to the benchmarks if you understand things so far.
As an example, consider an image of 4 by 4 pixels in width and height. For simplicity, the colour of each pixel is defined by a single byte.
This is allocated in memory as a 16 byte contiguous sequence (width x height = 4 x 4 = 16) in row-major order.
By convention, pixels in an image are identified by x- and y-coordinates, starting at 0,0 in the top-left and ending at (width-1), (height-1) at the bottom-right.
This is shown in a diagram, below. The value of each pixel is irrelevant; we are interested in the index of each pixel, i, and how it maps to x, y coordinates, as shown in the key.
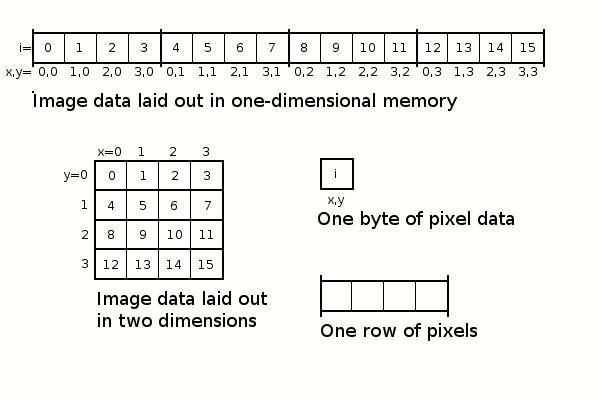
A marco will be created to map x, y coordinates to the pixel index in contiguous memory:
# define PixelIndex(image, x, y) ( ((y) * (image->width)) + (x) )
Some languages allow you to access multi-dimensional arrays without the need for such a macro, however it is important for this example that you are mindful that this is what is happening behind-the-scenes.
Now, consider that you might want to iterate over all the pixels in the image.
The simplest way would be to treat the array one-dimensionally:
for(i = 0; i < (image->width * image->height); i++)
{
color = image->pixels[i];
DoSomething(color);
}
This is great; each pixel is accessed sequentially in contiguous memory. The access pattern exploits spatial locality for optimal cache use.
However, consider what happens when you treat the array two-dimensionally (for a real-world example, you might do this for a PNG-style pre-compression filter).
for(x = 0; x < image->width; x++)
{
for(y = 0; y < image->height; y++)
{
i = PixelIndex(image, x, y);
color = image->pixels[i];
DoSomething(color);
}
}
The change in y coordinate on every iteration will produce an access pattern with low spatial locality. Remember in our macro each y coordinate is multiplied by image->width in the process of getting the array index:
# define PixelIndex(image, x, y) ( ((y) * (image->width)) + (x) )
Lets apply a hypothetical computer with a fast cache of 6 bytes (analogous to a CPU cache) and a slower buffer in which the image data resides (analogous to RAM) to illustrate the example.
This simplified cache system can only cache data in blocks of 6 bytes (a 6-byte cache line). In a more complicated example, the cache would have multiple small cache lines and more memory in total.
The following diagram highlights the accessed values during four iterations of the inner for(y) loop. It also displays a typical case of where cache misses can be expected.
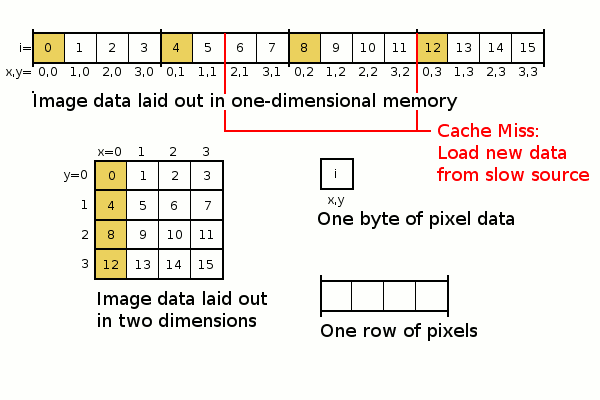
Notice that this access pattern has poor one-dimensional spatial locality. Subsequently, only one or two values are read until we experience a cache miss and the cache has to load fresh data from a slower source. This will cause about 12 cache misses for the entire 16 pixels.
Consider what happens if we change our example subtly to iterate first through y, and then through x.
for(y = 0; y < image->height; y++)
{
for(x = 0; x < image->width; x++)
{
i = PixelIndex(image, x, y);
color = image->pixels[i];
DoSomething(color);
}
}
The only difference is that the for(y) and for(x) statements have been reversed. But consider how the data is now accessed far more sequentially, exploiting spatial locality and therefore making better use of the cache.
The following diagram highlights the first four iterations of the inner loop again:
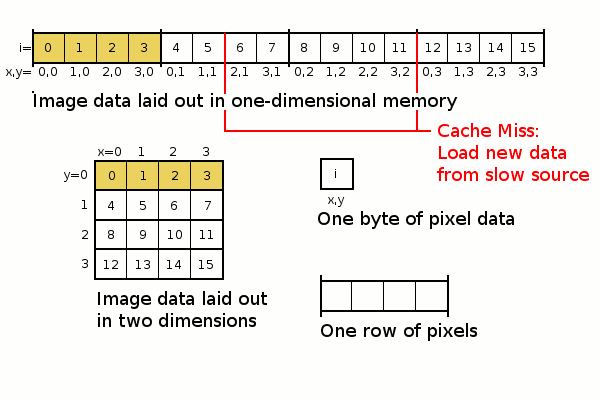
This time, we have had a successful cache hit for each of the four pixels accessed. We would only have three cache misses for the entire 16 pixels.
N.B. If you change the method of mapping of two-dimensional coordinates onto the one-dimensional array, e.g. so that y-coordinates are sequential rather than x-coordinates, obviously the situation reverses. However, the convention is to use sequential x-values as described, also known as row-major order. MATLAB and Fortran are notable exceptions; these languages use column-major order.
Benchmark
That's the theory. How does it hold up in practice?
Here's some C code, with compilation instructions in the comments.
If you have JavaScript enabled, the code below will have syntax highlighting.
Iterating through an Unsigned Char Array - locality_char.c
/*
Benchmark for http://www.tophatstuff.co.uk/?p=119
"Spatial Locality of Reference: an Efficient Access Pattern for
Cache Systems"
Compile and run:
gcc -O0 -Wall -Wextra -DX_FIRST locality_char.c -o locality_xfirst_char.elf
gcc -O0 -Wall -Wextra locality_char.c -o locality_yfirst_char.elf
echo "# width (bytes), width*height (bytes), time" > ./xfirst_char.txt
echo "# width (bytes), width*height (bytes), time" > ./yfirst_char.txt
./locality_xfirst_char.elf >> xfirst_char.txt
./locality_yfirst_char.elf >> yfirst_char.txt
*/
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <string.h> /* for memset */
#include <time.h>
# define ITERATIONS 50
# define MAX_WIDTH (5*512)
# define MAX_SIZE (MAX_WIDTH * MAX_WIDTH)
# define SIZE_STEP 32
# define PixelIndex(x, y, w) ( ((y) * (w)) + (x) )
int main(void)
{
clock_t start, end;
int i, j, k, x, y;
int width, height, size;
char byte;
unsigned char *pixels;
/* set up an "image" of one-byte pixels */
pixels = malloc(sizeof(char) * MAX_SIZE);
assert(pixels);
/* for multiple size images... */
for (i = SIZE_STEP; i < MAX_WIDTH; i += SIZE_STEP)
{
/* dimensions for this test */
width = height = i;
size = width * height;
assert(size <= MAX_SIZE);
/* clear the image */
memset(pixels, 0, sizeof(char) * size);
start = clock();
/* for each iteration... */
for (j = 0; j < ITERATIONS; j++)
{
#ifdef X_FIRST
/* this should be slow */
for (x = 0; x < width; x++)
{
for (y = 0; y < height; y++)
{
k = PixelIndex(x, y, width);
byte = pixels[k];
}
}
#else
/* this should be faster */
for (y = 0; y < height; y++)
{
for (x = 0; x < width; x++)
{
k = PixelIndex(x, y, width);
byte = pixels[k];
}
}
#endif
}
end = clock();
/* print image size and time for ITERATIONS iterations */
printf("%d, %d, %f\n",
width,
(width * height),
((double)(end - start)) / ((double) CLOCKS_PER_SEC));
fflush(stdout);
}
return 0;
}
Iterating through a Signed Integer Array - locality_int.c
/*
Benchmark for http://www.tophatstuff.co.uk/?p=119
"Spatial Locality of Reference: an Efficient Access Pattern for
Cache Systems"
Compile, run and plot:
gcc -O0 -Wall -Wextra -DX_FIRST locality_int.c -o locality_xfirst_int.elf
gcc -O0 -Wall -Wextra locality_int.c -o locality_yfirst_int.elf
echo "# width (ints), width*height (ints), time" > ./xfirst_int.txt
echo "# width (ints), width*height (ints), time" > ./yfirst_int.txt
./locality_xfirst_int.elf >> xfirst_int.txt
./locality_yfirst_int.elf >> yfirst_int.txt
*/
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <string.h> /* for memset */
#include <time.h>
# define ITERATIONS 20
# define MAX_WIDTH (6*512)
# define MAX_SIZE (MAX_WIDTH * MAX_WIDTH)
# define SIZE_STEP 64
# define PixelIndex(x, y, w) ( ((y) * (w)) + (x) )
int main(void)
{
clock_t start, end;
int i, j, k, x, y;
int width, height, size;
int value;
int *pixels;
/* set up an "image" of one-byte pixels */
pixels = malloc(sizeof(int) * MAX_SIZE);
assert(pixels);
/* for multiple size images... */
for (i = SIZE_STEP; i < MAX_WIDTH; i += SIZE_STEP)
{
/* dimensions for this test */
width = height = i;
size = width * height;
assert(size <= MAX_SIZE);
assert(size > 0);
/* clear the image */
memset(pixels, 0, sizeof(int) * size);
start = clock();
/* for each iteration... */
for (j = 0; j < ITERATIONS; j++)
{
#ifdef X_FIRST
/* this should be slow */
for (x = 0; x < width; x++)
{
for (y = 0; y < height; y++)
{
k = PixelIndex(x, y, width);
value = pixels[k];
}
}
#else
/* this should be faster */
for (y = 0; y < height; y++)
{
for (x = 0; x < width; x++)
{
k = PixelIndex(x, y, width);
value = pixels[k];
}
}
#endif
}
end = clock();
/* print image size and time for ITERATIONS iterations */
printf("%d, %d, %f\n",
width,
(width * height),
((double)(end - start)) / ((double) CLOCKS_PER_SEC));
fflush(stdout);
}
return 0;
}
Running both programs will give you four files, with several data points.
If you have a large CPU cache, you may like to extend MAX_WIDTH to fit. If you have a fast CPU, you may like to increase ITERATIONS.
Benchmark Results
Raw results are given here.
Here's a graph of array width against time for locality_char.c:
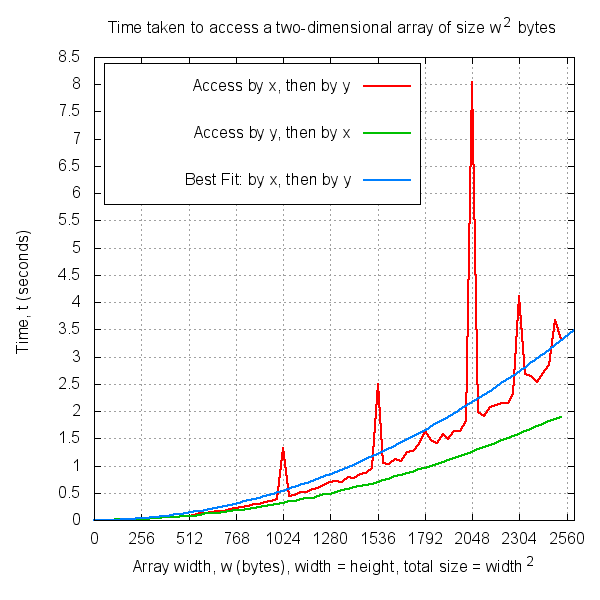
I used this gnuplot script to plot the graph.
Gnuplot gives the line of best fit as
y = mx^2 where m = 5.15107e-07 +/- 2.854e-08 (5.54%)
Here's a graph of array width against time for locality_int.c:
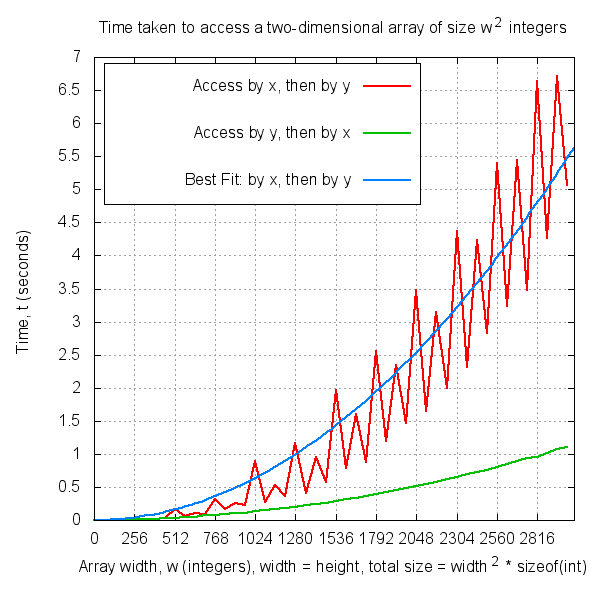
I used this gnuplot script to plot the graph.
Gnuplot gives the line of best fit as
y = mx^2 where m = 6.0499e-07 +/- 2.556e-08 (4.225%)
N.B. the two graphs are not directly comparable.
The graphs certainly show something interesting!
Not only do the two graphs show that accessing an array in a for(y), for(x) loop is the faster option, but the graphs show spikes at certain points.
Looking at the locality_char.c benchmark, the first spike occurs at an array width of 1024. Squaring this value gives an array size of 1024x1024 bytes, or one megabyte. This is the exact size of my CPU's Level 2 Cache! (Yes, my computer is old!). Therefore, it is reasonable to assume that these spikes correlate to cache sizes.
If the benchmark continued until it used over 2GB of memory and I ran out of RAM and started paging to disk in the same way that my Level 2 cache was exhausted, I predict you would see a similar pattern emerge. Similarly you would notice an effect if you zoomed in at the area where my Level 1 CPU cache would become exhausted.
Using lines of best fit to smooth out the spikes in both benchmarks, we can estimate the performance gain in real terms.
For a typical value, such as an array of 2048 by 2048, we find:
- In locality_char.c, looping through an Unsigned Char array by y and then x gives a 1.7x speedup compared to looping by x and then y.
- In locality_int.c, iterating through a Signed Integer array by y and then x gives a 5.0x speedup compared to looping by x and then y.
With these results, it is clear how the pattern of memory access in a cache system can be vital to run-time performance in some cases.
Real World Application: Paeth Filter
The implications of this study can be applied to real-world applications.
For one application, I was filling a 2D array of 2048x2048 floating-point numbers with 10-octaves of 3D simplex noise. The approach described in this study resulted in a 1.03x speedup for this specific case. Most of the time was spent computing the simplex noise.
For another application, I was applying a Paeth filter to a 2048x2048 array of bytes. Paeth filters are used in PNG images to make the file more compressible. I found that the approach described by this study led to a full 4.47x speedup! In this case, the bottleneck was not expensive instructions but memory bandwidth.
Compiling with gcc -O2 level optimisation increased the gain to a 6.50x speedup over the alternative.
To try it for yourself, download and run paeth.c.
Given that there is no trade-off with readability or complexity, changing the order of nested loops when accessing memory is an easy improvement that can deliver massive gains in specialised cases.
Further Reading
How the CPU cache size affects programs can often be surprising and unintuitive. Here's some further reading:
- Gallery of Processor Cache Effects, Igor Ostrovsky (lovely graphs)
- Stack Overflow discussion: Why is one loop so much slower than two loops? This picks up on memory alignment in the accepted answer.
- AMD, Processor Cache 101: How Cache Works. In-depth article that dips into cache coherency and "false sharing" which has massive implications for multithreaded programs.
If you enjoyed this article, you might also enjoy Optimal Compression for Binary Data: "How I managed to compress a 5mb map into just 36kb with two simple techniques"
Feedback welcomed: e-mails to Ben Golightly (ben@tophatstuff.co.uk)
Advertisement Looking for high-quality unmanged VPS hosting?Full root access, managed DNS
UK, USA and JP datacentres
2GB of RAM,
48GB SSD storage,
3TB bandwidth
$20/month
Linode.com
Stay Subscribed
, subscribe to the RSS feed or get updates by e-mail.
You can also contact me directly - I make an effort to reply to every e-mail.
